Monte Carlo Simulation (“MCS”) is an advanced computational technique used to model the probability of different outcomes in a process subject to uncertainty. Initially developed during the mid-20th century and famously used in nuclear research, MCS has become an indispensable tool across industries such as finance, engineering, risk management, supply chain, and scientific research. By assigning probability distributions to key variables, Monte Carlo models enable professionals to assess risks, forecast uncertainties, and enhance strategic decision-making with empirical precision.

Monte Carlo simulation is particularly valuable in financial modeling, where it facilitates risk-adjusted valuations and scenario-based decision analysis. In investment banking, for example, MCS is widely used to simulate potential Net Present Values (NPVs) under varying economic conditions, allowing for more comprehensive investment evaluations. Studies show that over 75% of Fortune 500 companies rely on Monte Carlo techniques for risk assessment and financial planning.

Monte Carlo Simulation in Option Pricing

One of the most prominent applications of Monte Carlo Simulation is in option pricing analysis. In the context of financial derivatives, MCS is employed to simulate asset price trajectories and determine expected option payoffs under stochastic market conditions. The final option value is obtained by averaging the simulated payoffs, adjusted for risk-neutral probabilities.

The Role of Geometric Brownian Motion (GBM)

Monte Carlo simulations for option pricing frequently assume that stock prices adhere to a Geometric Brownian Motion (GBM) stochastic process. GBM incorporates both a deterministic growth trend and stochastic volatility, making it well-suited for modeling financial asset behavior.

The mathematical representation of GBM is:

Where:

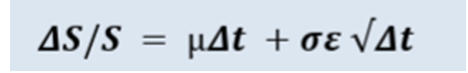
S = Current stock price

µ = Expected return

σ= Expected volatility

t = expected term (in years)

ξ= Wiener process (random variable following a normal distribution)

This formulation accounts for a continuous drift (representing the expected return) and random market shocks (capturing price fluctuations), making it a powerful tool for pricing contingent claims.

Enhanced Inputs to the Monte Carlo Model

Monte Carlo simulations rely on a comprehensive set of inputs akin to other option pricing models but with added flexibility. These include:

• Stock price
• Exercise price
• Volatility
• Expected term
• Risk-free rate
• Dividend yield
• Probability distribution assumptions

A distinctive feature of Monte Carlo Simulation is its reliance on advanced probability distributions to model uncertainties. Commonly utilized distributions include:

• Lognormal Distribution: Preferred for modeling asset prices due to its non-negativity and right-skewed nature.
• Normal Distribution: Often applied in revenue and profitability forecasts, enabling symmetrical outcome projections.
• Triangular and Uniform Distributions: Used in situations with limited historical data, providing approximations for uncertain variables.

Recent advancements in financial modeling have introduced stochastic volatility models such as the Heston Model, which incorporates volatility dynamics into Monte Carlo simulations, improving pricing accuracy for exotic options. According to recent industry reports, over 80% of hedge funds now integrate Monte Carlo techniques into their derivative pricing strategies to account for market anomalies.

Modern Applications in Financial Reporting & Valuations

Monte Carlo Simulation has become the preferred methodology for valuing Employee Stock Options (ESOPs) and complex financial instruments with market-based performance conditions. Key use cases include:

Multi-Factor ESOP Valuation: MCS effectively models ESOPs with both market and performance-based vesting conditions, such as stock price appreciation coupled with revenue milestones.
Volatility Adjustments for Public vs. Private Entities: The model accounts for heightened volatility in publicly traded securities versus privately held firms. Unlike the binomial option pricing model, MCS incorporates stochastic elements that better capture market uncertainties.
Early Exercise Behavior: MCS allows the modeling of early exercise scenarios, a crucial factor in ESOPs where employees may exercise options ahead of scheduled vesting dates.
Capped Payout Conditions: For Stock Appreciation Rights (SARs) or capped options, MCS can impose payout ceilings dynamically, ensuring precise valuation.
Hybrid Probability Distributions: Monte Carlo models can accommodate multiple probability distributions simultaneously, such as a lognormal distribution for stock prices and a normal distribution for operating profit, to simulate dual-dependent vesting conditions.

Recent regulatory changes under IFRS 2 and ASC 718 have further emphasized the importance of Monte Carlo models in financial reporting, ensuring compliance with fair value measurement guidelines for complex share-based compensation structures.

Limitations and Considerations in Monte Carlo Simulation

While Monte Carlo Simulation provides enhanced valuation insights, it is not without challenges:

Computational Intensity: Running high-fidelity simulations requires significant computational resources, making the model resource-heavy for large-scale financial applications. However, recent advancements in cloud computing and parallel processing have mitigated these constraints.
Model Sensitivity: Monte Carlo results are highly sensitive to input assumptions, particularly in defining volatility estimates and probability distributions. Poorly specified inputs can distort valuations, leading to unreliable outputs.
Data and Calibration Challenges: Selecting appropriate probability distributions requires substantial historical data, which may not always be available for private companies or emerging markets.
Time-Intensive Analysis: Running thousands of simulations for robust pricing estimates can be time-consuming, necessitating algorithmic optimizations to enhance efficiency.

Conclusion: The Evolving Role of Monte Carlo Simulation

Monte Carlo Simulation continues to be a cornerstone of financial risk management, option pricing, and investment analysis. Its ability to incorporate complex probability distributions and stochastic volatility models makes it an indispensable tool for modern finance professionals.

Emerging trends such as machine learning-driven Monte Carlo simulations and AI-powered financial modeling are further augmenting its predictive capabilities, offering more granular insights into risk exposure and valuation dynamics. A recent study by the Financial Stability Board (FSB) highlights that AI-integrated Monte Carlo techniques have improved risk assessments by 35% in volatile market conditions.

As regulatory requirements evolve and financial markets become increasingly complex, Monte Carlo Simulation remains a critical tool for professionals navigating uncertainties, optimizing investment strategies, and ensuring compliance with evolving financial standards.

Share via